フーリエ空間イメージング

レンズのフーリエ変換作用を用いることで，物体の透過光や散乱光の角度依存性を簡便に観測できます．フーリエ面を直接観る系になるため，フーリエ空間（Fourier space）或いは，波数空間（k-space），後方焦点面（Back focal plane）イメージングとも呼ばれます．本記事では，その原理を解説します．同様の原理は，顕微鏡のKöhler照明や，電子顕微鏡の電子線回折にも利用されているため，ナノフォトニクス分野の材料屋さんにとっては非常に重要なコンセプトです．

フーリエ空間イメージングの原理は，近軸近似（paraxial, Gaussian Optics）の下で，簡単な光線追跡で説明できます．焦点距離 f のレンズに対して，中学校で習う近軸光線の基本的なルール（レンズの焦点を通る光線は光軸に平行に進む，光軸に平行に入射した光は焦点を通る，レンズの中心を通る光は直進する，等）を下に，左側焦点に配置された物体（矢印）から出た光の光線を作図すると以下のようになります．

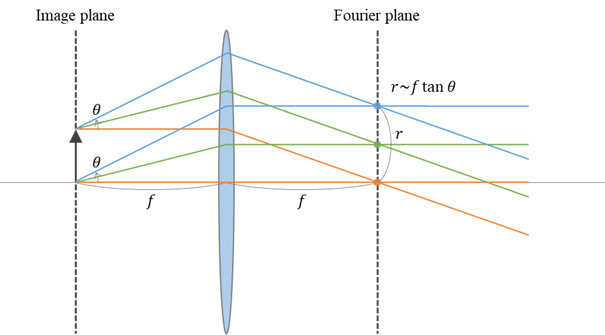
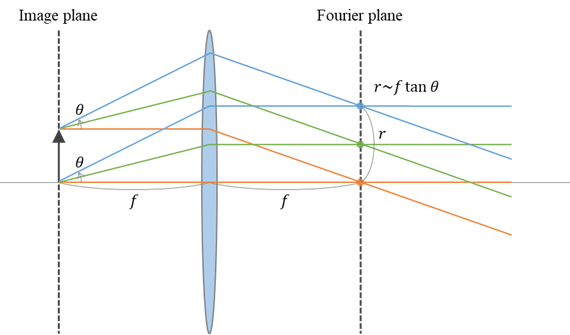
まず，物体の位置，すなわち実空間（Image plane）で同じ点から出た光は平行光となり，レンズ後方では像を結びません．一方，レンズの後方焦点面では，同じ角度（θ）に射出された光が同じ点に結像している（交差する）ことがわかります．矢印の根本から出た光も，先端から出た光も，後方焦点面では角度のみに依存して中心からの距離が決まっていることがポイントです．近軸光線を仮定した作図では，後方焦点での結像位置（光軸からの距離）r はf tanθ で表されますが，厳密にはr = f sinθ となることに注意して下さい．θ が十分小さい場合，sinθ ~ tanθ ~ θ なので矛盾はありません．

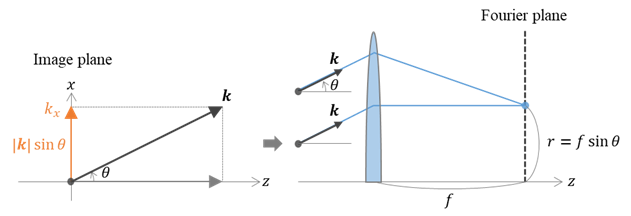
この作用がレンズのフーリエ変換作用と呼ばれる理由は，射出された光の波数ベクトルを考えるとよくわかります．以下のように，座標軸を取り，射出された光の波数ベクトルを k とすると，面内ベクトル k_x は |k|sinθ で表されます．従って，後方焦点面での結像位置 r = f sinθ は，実空間における面内波数に比例する物理量となります．すなわち，位置情報が空間周波数に変換されており，フーリエ変換に相当することがわかります．定量的には，光学の教科書を参照されるとよいと思います．

原理上は以上の通りで，実験で観測するには，後方焦点面がCCD等のイメージセンサーに像を結ぶように，更に１～２枚のレンズでリレーします．アライメントには，特定の角度で光を透過・反射するグレーティング等を用いると良いでしょう．

同様の原理で，画像の空間周波数フィルタリング [Thorlabs, フーリエ光学教育キット] や，二次元フォトニック構造の分散関係測定 [Nat. Nanotech. 13, 1042-1047 (2018)] が可能です．筆者の研究では，顕微鏡と組み合わせることで，単一のナノ粒子の散乱光の角度依存性を測定しています．また，電子顕微鏡における電子線回折像は，回折された電子線のパターンを逆空間で観測します．これも，後方焦点面を蛍光板に結像させることで実現していますが，回折角度が蛍光板において中心からの距離として現れていると見ると，より理解しやすいのではないでしょうか．